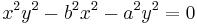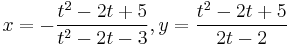Cruciform curve

The cruciform curve, or cross curve is a quartic plane curve given by the equation

$x^2y^2-b^2x^2-a^2y^2=0 \,$

where a and b are two parameters determining the shape of the curve. The cruciform curve is related by a standard quadratic transformation, x ↦ 1/x, y ↦ 1/y to the ellipse a²x² + b²y² = 1, and is therefore a rational plane algebraic curve of genus zero. The cruciform curve has three double points in the real projective plane, at x=0 and y=0, x=0 and z=0, and y=0 and z=0.

Because the curve is rational, it can be parametrized by rational functions. For instance, if a=1 and b=2, then

$x = -\frac{t^2-2t%2B5}{t^2-2t-3}, y = \frac{t^2-2t%2B5}{2t-2}$

parametrizes the points on the curve outside of the exceptional cases where the denominator is zero.